27313번: 효율적인 애니메이션 감상
첫 번째 줄에 한별이가 봐야 하는 애니메이션의 개수 $N$, 한별이가 애니메이션을 보는 데에 사용할 수 있는 시간을 나타내는 정수 $M$, 한별이가 동시에 볼 수 있는 애니메이션의 개수 $K$가 공백
www.acmicpc.net
이분탐색 문제입니다.
이 문제에 이분탐색을 어떻게 적용할 수 있을까 엄청 고민했는데,
일단 정렬하고 생각해봤습니다.
애니메이션을 보는데 걸리는 시간은 보는 애니 중 가장 길이가 긴 것입니다.
따라서 가장 긴 것만 본다고 가정합니다.
또한, 애니메이션은 항상 k개씩 봐야지 가장 많이 볼 수 있습니다.
따라서 k는 고정입니다.
그럼 애니메이션을 몇 개 볼 수 있는지에 대해서 이분탐색을 할 수 있습니다.
7 10 2
2 3 1 4 5 6 7위와 같이 입력이 들어올 경우
1 2 3 4 5 6 7로 정렬될 겁니다.
이분탐색에서 시작은 1, 끝은 7일 것이며, 중간은 4가 됩니다.
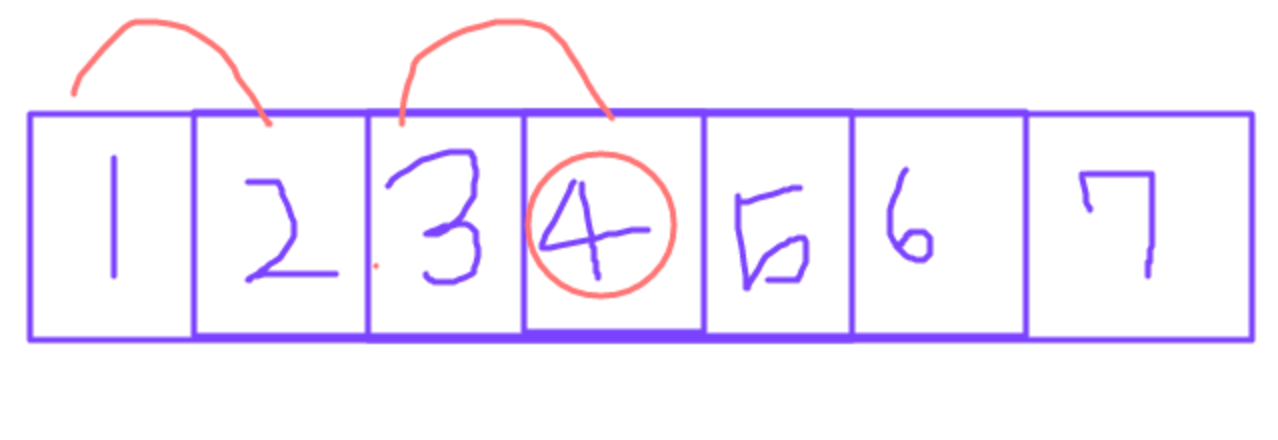
애니를 4편 봤지만 걸린 총 시간은 6으로, 이는 m값인 10보다 작습니다.
시작점을 중간으로 옮겨주면
시작은 4, 끝은 7, 중간은 5가 됩니다.
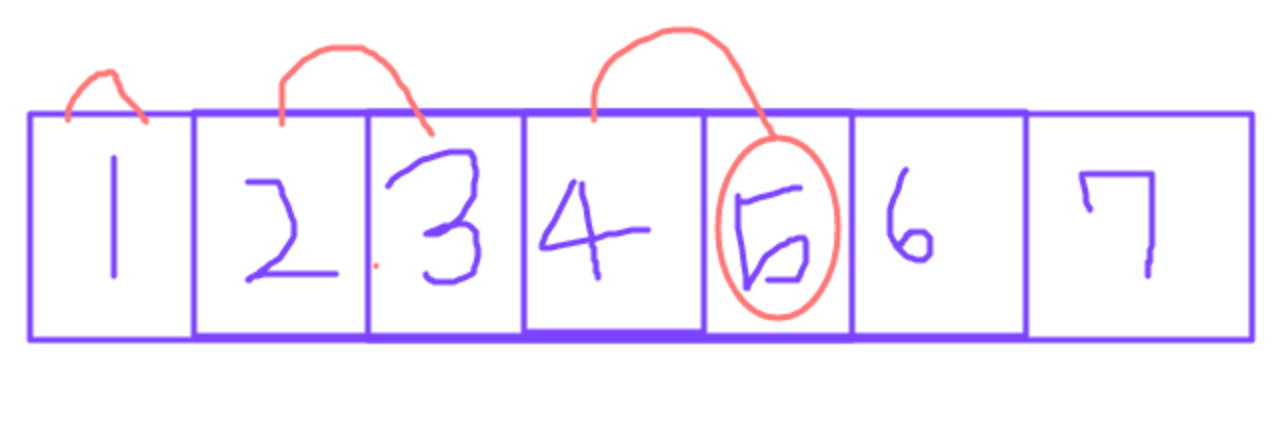
애니 5편을 봤을 때 총 걸린 시간은 9로, 이는 m값인 10보다 작습니다.
시작점을 5로, 이에 중간을 6으로 옮기면 총 시간은 12로, m보다 큽니다.
이렇게 이분탐색을 진행하면 0번째부터 시작점까지의 영화를 모두 볼 수 있습니다.
사이드케이스로,
1 1 1
10과 같은 입력이 들어올 경우, 0번째의 원소 하나만으로도 m값을 넘기기에 이를 신경써야합니다.
#include <iostream>
#include <algorithm>
#include <cmath>
using namespace std;
long long arr[100000],n,m,k,tmp,ans = -1,fir,e,mid, coun;
int main() {
ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
cin>>n>>m>>k;
for(int i = 0; i < n; i++) cin>>arr[i];
sort(arr, arr + n);
fir = 0;
e = n;
for(int i = 0; i < log2(n); i++) {
tmp = coun = 0;
mid = (fir + e) / 2;
for(int j = mid; j >= 0; j -= k) {
coun++;
tmp += arr[j];
}
if(tmp <= m) {
ans = max(ans, coun);
fir = mid;
}
else {
e = mid;
}
}
if(arr[fir] > m) cout<<0; //가장 짧은 애니도 m보다 길 경우
else cout<<fir + 1;
}
'백준' 카테고리의 다른 글
| [C언어/C++] 17135 캐슬 디펜스 (0) | 2023.08.17 |
|---|---|
| [C++] 백준 | 1790번 수 이어 쓰기 2 (0) | 2023.02.15 |
| [C++] 백준 | 1018번 체스판 다시 칠하기 (0) | 2023.02.08 |
| [C++] 백준 | 19590번 비드맨 (0) | 2023.02.06 |
| [C++] 백준 | 17143번 낚시왕 (0) | 2023.02.03 |